Hiraoka Group
Applied Mathematics
Research Overview
Topological data analysis is an emerging concept in applied mathematics in which we characterize “shape of massive and complex data” using topological methods. In particular, persistent homology and mapper are nowadays applied to a wide variety of scientific and engineering problems including materials science, life science and social networks etc. By combining various mathematics such as topology, representation, statistics and probability theory, our group has succeeded in making topological data analysis powerful and general methods for practical problems. For example, we have applied these methods to structural analysis in materials science so far, and the developed techniques by our group are expected to be a key technology for materials informatics. In ASHBi, we aim to understand the principle of species differences among humans, non-human primates, and rodents by applying topological data analysis, dynamical system, and machine learning to multi-species, multi-cell types, multi-hierarchical omics information. This analysis will also be extended into the identification of the principles for the species differences on the scales of time and physical dimensions in development and growth. We hope that interdisciplinary researches between biology and mathematics in ASHBi will develop powerful advanced mathematical methodology for massive and complex biological data, and contribute to the progress of life science.
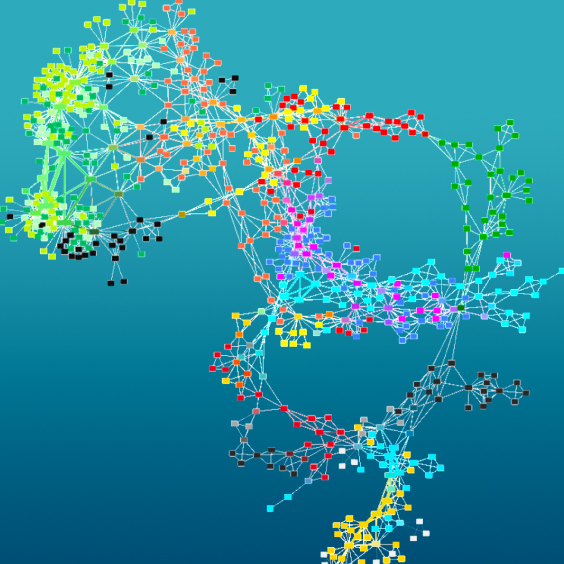
Figure 1: Topological clustering on single cell analysis data of monkeys by mapper (Left: cell clusters. Right: Gene clusters)
Members

Yasuaki Hiraoka
- Position
- Professor
- Laboratory Website
-
https://sites.google.com/view/hiraoka-lab/
-
Yusuke Imoto
Associate Professor
-
Killian Francis Meehan
Program-Specific Researcher
-
Jun Okamoto
Program-Specific Researcher
-
Yuya Tokuta
Program-Specific Researcher
-
Sebastián Elías Graiff Zurita
Program-Specific Researcher
Publications
Y Imoto, Y Hiraoka. V-Mapper: topological data analysis for high-dimensional data with velocity. Nonlinear Theory and Its Applications (NOLTA), Vol. 14 (2), pp. 92-105, 2023.
Yusuke Imoto, et al. Resolution of the curse of dimensionality in single-cell RNA sequencing data analysis. Life Science Alliance 5(12) e202201591-e202201591. 2022.
Obayashi, Y. Hiraoka, M. Kimura. Persistence Diagrams with Linear Machine Learning Models. J. Appl. and Comput. Topology (2018), 1, 421–449.
Kusano, K. Fukumizu, and Y. Hiraoka. Kernel method for persistence diagrams via kernel embedding and weight factor. Journal of Machine Learning Research 18 (2018) 1-41.
Kimura, I. Obayashi, Y. Takeichi, R. Murao and Y. Hiraoka. Non-empirical identification of trigger sites in heterogeneous processes using persistent homology. Scientific Reports 8, Article number: 3553 (2018).
Mohammad Saadatfar, Hiroshi Takeuchi, Nicolas Francois, Vanessa Robins, and Yasuaki Hiraoka. Pore configuration landscape of granular crystallisation. Nature Communications. 8:15082 (2017).
Hiraoka, T. Nakamura, A. Hirata, E. G. Escolar, K. Matsue, and Y. Nishiura. Hierarchical structures of amorphous solids characterized by persistent homology. Proceedings of the National Academy of Sciences of the United States of America 113 (2016), 7035–7040.
