Collaborating Laboratories・共同研究ラボ
Our most interest is to know how “WE (human being)” are created. BiMed-Math Lab aims to understand the self-organizing system of life organisms via interdisciplinary approaches: mathematical modeling/analysis, data analysis, bio-experiment and clinical trial/analysis. The process of human development is the harmony of temporal and spatial dynamics of all life units such as gene, cell, tissue and organs. Although a cell function is initially regulated by the blueprint of genetic information and the times of genetic analysis has been arrived, it is still far from to know all human biology. This is because the human completes its system via the process of self-organization which is a (beautiful) magic.

生命のパターン形成
Pattern formation is one of the representative self-organizing methods by which cells regulate their functions each other and determine their fate in right time and right place. Pattern formation is universal phenomenon found in not only multicellular systems but also in nuclei and single cells. This means that if we can find the essential mechanism of pattern formation, we may be able to regulate cell function through the mechanism of pattern formation, which can lead to a new clinical treatment in medicine. Thus, with the keyword of pattern formation, I have extensively studied to elucidate how cells regulate their function temporally and spatially via the process of spatial patterning, from the scale of chromatin to the scale of tissue and organs, by using the framework of mathematical modeling. BiMed-Math Lab’s strength in research is that we do not limit research targets to a specific scale of life unit. Once the biological languages are changed to the mathematical language, they are the same for us.
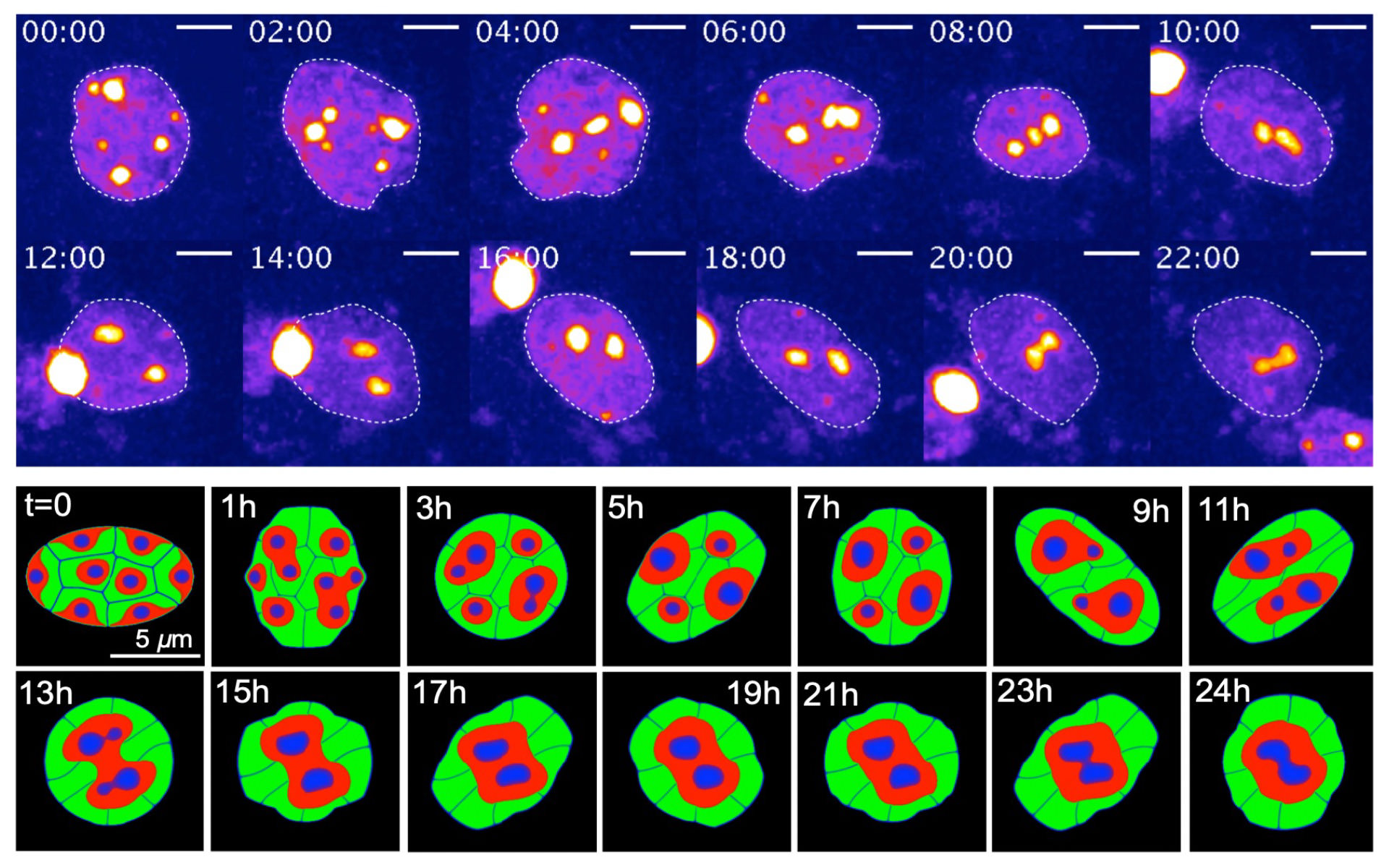
細胞核内クロマチンの空間再編
The spatial reorganization of chromatins is deeply involved in cell function. One of the most remarkable examples of spatial genomic reorganization is the rod photoreceptor cell differentiation in mammals, including mice. The inverted architecture found in adult mouse rod cells is formed through the reorganization of the conventional architecture during terminal differentiation. However, the mechanism underlying these changes remained largely unknown. In this research, we have found that dynamic deformation of nucleus is critical to induce the reorganization of chromatin architecture. In this work, the concept of mathematical tool was very challenging to apply to chromatin dynamics, so that the mathematical idea was able to suggest unexpected possibility, which led to a new biological discovery.
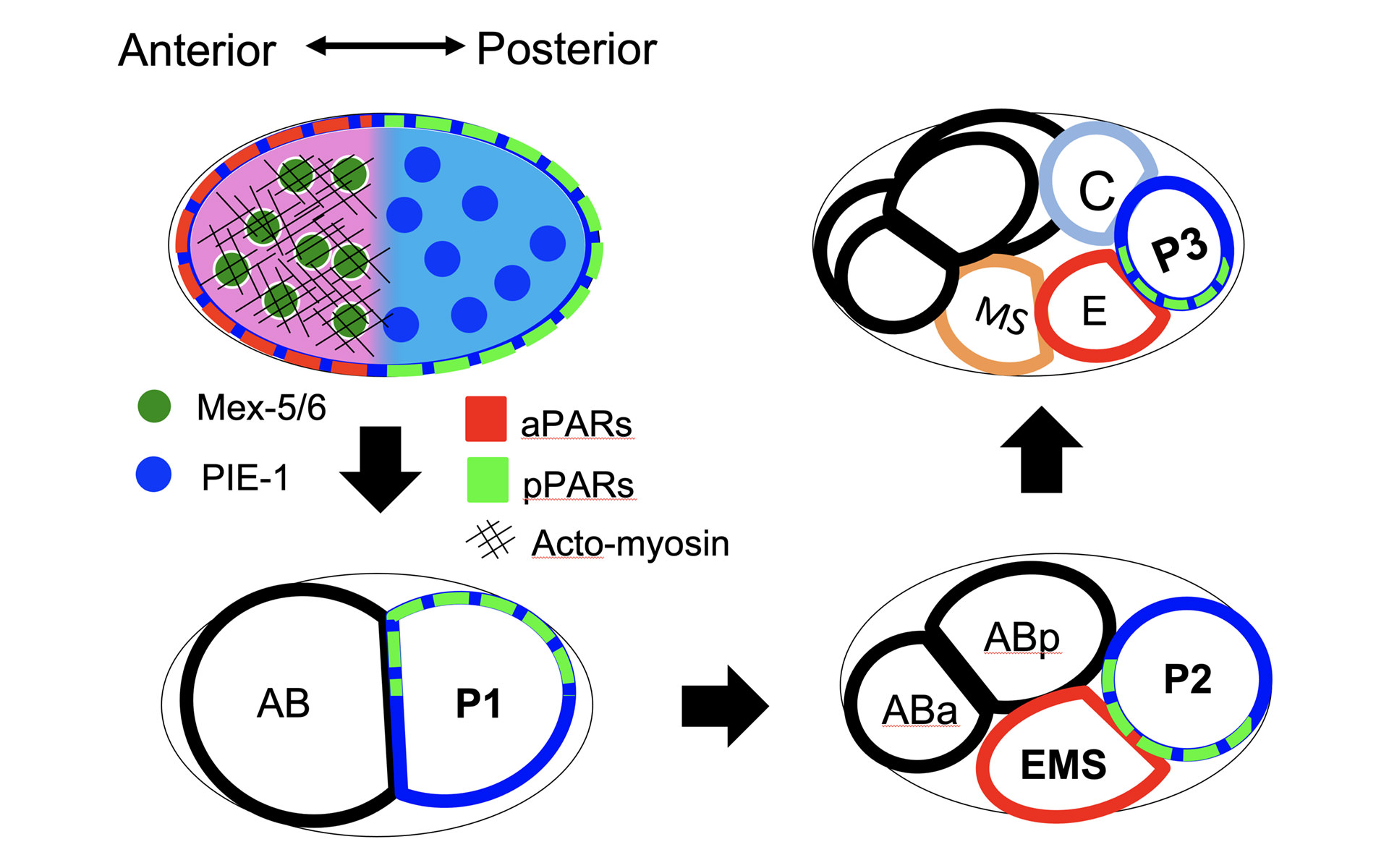
非対称細胞分裂と極性形成
The human body is composed of 250~300 kinds of cells with different functions and sizes, which are diversified from a single fertilized egg cell during development. One of the widespread mechanisms for generating cell diversity is asymmetric cell division. A mother cell divides into two dissimilar daughter cells, which subsequently develop completely different properties. The phenomenon of asymmetric cell division is the ultimate spatiotemporal control of the cell and it delivers integrated understanding of how life self-organizes itself. Thus, the elucidation of the key mechanism of asymmetric cell division leads to find key biological traits for understanding the basis of human development. In this research, we extensively studied the basal mechanism of polarity formation (asymmetry of bio-chemical substrates) generated in both membrane and cytosol of mother cell by bio-chemical and bio-mechanical approaches. In particular, we have found a general mechanism by which a mother cell makes the asymmetry of cytoplasmic proteins using the polarity of membrane proteins. We also extended it with respect to cell geometry and explored how the asymmetry of daughter cell size can be affected by the size or shape of the mother cell. Currently, with collaboration of bio-experiment we are extending this research not only for the single cell stage (the first mother cell stage) but also for the multicellular stage where asymmetric cell divisions are repeated. Our near future plan is to lead the way in developing a theoretical approach for asymmetric cell division at the multicellular stage, and to understand the entire mechanism of asymmetric cell division.
多層的組織構造におけるパターン形成の解明
ヒトの初期発生の統合的理解

数理医学
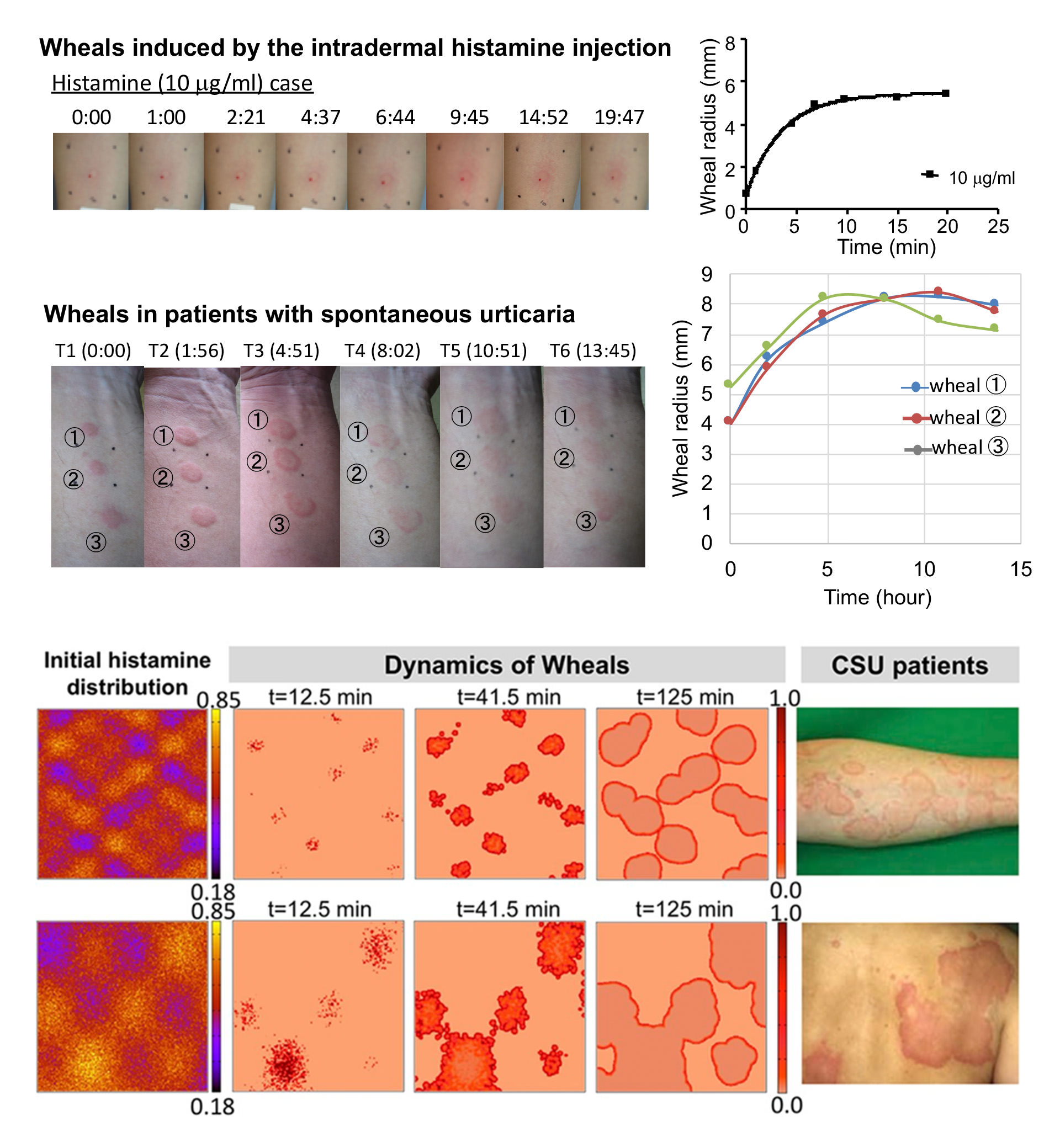
形から紐解く数理皮膚医学
The skin is the largest organ of human body and plays a very important role in the homeostasis of the life system of human. Nonetheless, the medical treatment and the mechanism of skin diseases, especially refractory skin disease such as Urticaria, remains a major issue. This is because there are no animal models for biological experiments (of course, human body cannot be used!). It thus makes a critical difficulty to find the underlying mechanism of bio-chemical dynamics of the skin disease. Thus, to overcome such problems, we have caused a change of thinking and used the inverse approach of conventional mathematical modeling. With this approach, we have found that the inhibition regulatory of histamine release from the mast cell plays a critical role in generating the multifarious eruption of urticaria, which had been a mystery for a long time in medicine. The idea of inhibition regulatory was completely unexpected finding which medical doctors have never thought. In this study, a mathematical model has played a role in connecting biology and clinical medicine. (Mathematical Dermatology: https://www.math-dermatology.com)
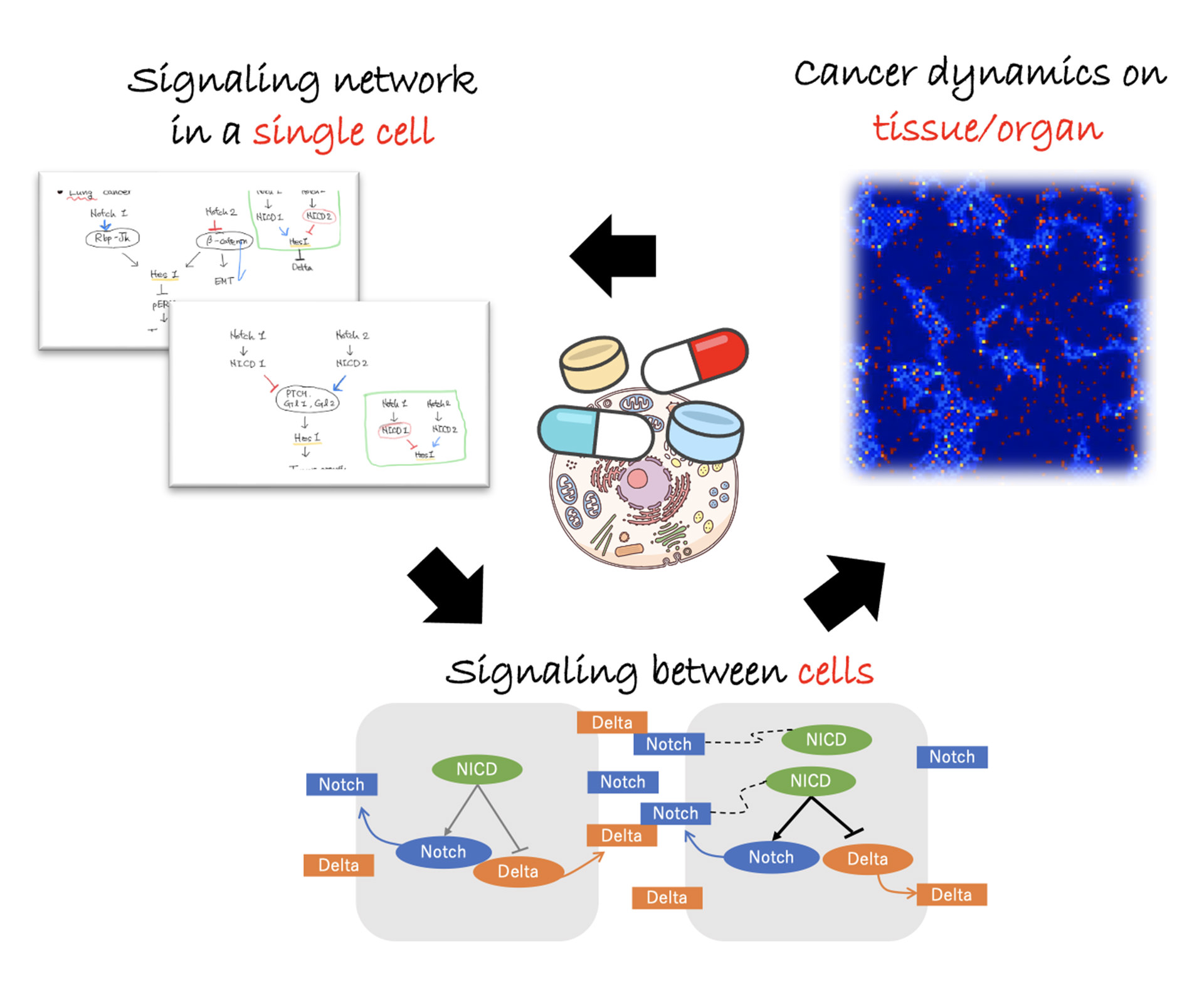
最適細胞治療法の開発
The development of cellular therapy in immune system diseases, including cancer, has gained momentum in recent years. In this study, we aim to establish a cellular therapeutic platform by integrating intra-/inter- cellular network and cell-to-cell dynamics. Recently, we are focusing on global dynamics of brain and lung cancers on tissue level with a hierarchical mathematical model based on intra-/inter- notch signaling network. Based on a mathematical tool, we propose new findings for the effective treatment of cancer.

空間数理免疫学
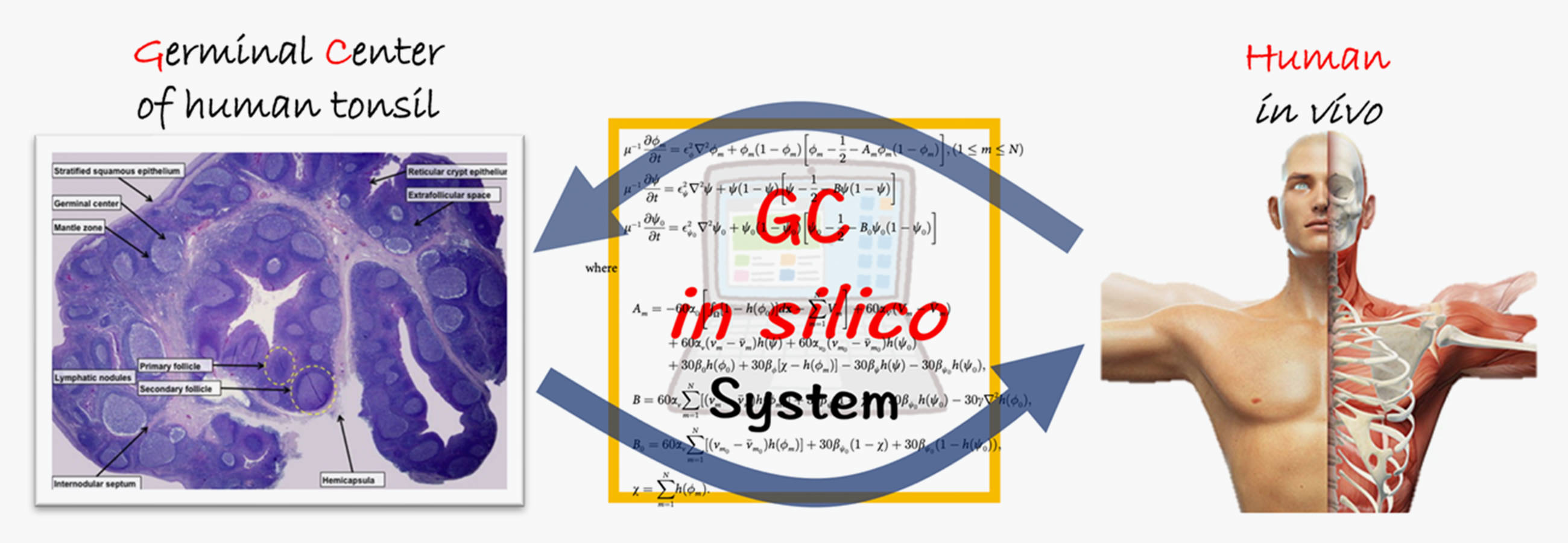
In the case of human immune system or immune system diseases, there exist cases in which the pathogenesis in vivo is unknown due to the lack of appropriate disease model animals, and the understanding of the pathogenesis and treatment are not yet established. Thus, we want to find a breakthrough that can capture the time series of immune responses from snapshot specimen information to solve the problems of human immunology, which are limited to experimental approaches and for which all in vivo spatiotemporal data cannot be obtained. In this study, we propose a new mathematical fusion approach based on an unconventional way of thinking to solve these problems and construct a methodology of mathematical immunology that can serve as a foundation for solving difficult problems in human immunology. The aim of this project is to develop a method to analyze the morphogenesis of germinal center (GC) of lymph node, which is the core of immune response regulation, using human tonsil specimens to analyze the time series of germinal center response in vivo. In particular, by building a framework of universally applicable fusion approaches, we will construct a general fusion method that can be applied to various issues in human immunology and human biology, not limited to a germinal center system.
ヒトの免疫系又は免疫系疾患の場合,適切な疾患モデル動物がなく生体内での発症機序が不明で,病態の理解と治療が未確立な場合が存在します.このように実験的アプローチだけでは解決の糸口が限られ,生体内の時空間的全てのデータを得ることができないヒト免疫学の課題に対して,スナップショットの検体情報から免疫応答の時系列を捉えることができる突破口はないでしょうか.本研究では,これらの課題解決に向け, 常識に囚われない発想の転換に基づく新しい数理融合アプローチを提案し,ヒト免疫学の難題解決の基盤となる数理免疫学の方法論を構築しています.免疫応答制御の中核となるリンパ節の胚中心(Germinal Center:GC)の形態形成を具体的な研究対象とし,生体内胚中心反応の時系列をヒト扁桃検体を用いて数理と実験の融合的アプローチの解析手法の開発を行っています.特に,普遍的に応用可能な融合アプローチの骨格を構築することで,胚中心に限らず,ヒト免疫学及びヒト生物学の様々な課題に展開していくことができる汎用的融合手法を構築していきます.

ネットワーク構造と生命の多様性
In this study, we aim to understanding the universality linking intracellular networks and differentiation decisions of cell groups. In particular, we are currently focusing on the process of germ cell differentiation with comparing mouse and human. To elucidate the underlying mechanism of Primordial Germ Cell(PGC) differentiation, we developed a multi-scale mathematical model linking a gene expression data, gene networks within a single cell, and the dynamics of cell populations.
本研究では、細胞内ネットワークと細胞群の分化の決定との普遍性の解明を目指しています。特に、生殖細胞の分化過程に着目し、マウスとヒトの比較研究を行っています。原始生殖細胞(PGC)の分化のメカニズムを解明するために、遺伝子発現データ、単一細胞内の遺伝子ネットワーク、細胞集団のダイナミクスを結びつけたマルチスケール数理モデルを開発しました。


データ記述に基づく数理モデル学と数理実験科学
Through the construction of a novel methodological fusion of cutting-edge data science and mathematical modeling, this research aims to construct an in-silico system that enables biological experiments to be performed on a personal computer as if they were conducted in a real experimental system.
If this framework can be constructed, it will not only be a low cost, but will also enable experiments to be conducted under conditions that are difficult in real biological experiments and is expected to make a significant contribution to the creation of new biological knowledge.
本研究では、最先端のデータ科学と数理モデリングの斬新な手法的融合手法の構築を通じて、まるで実際の実験系で行われる生物実験をパソコン上で可能とするシステムの構築を目指しています。この枠組みが構築できれば、コストが安いだけではなく、現実の生物実験で難しいような条件でも実験が可能となり、新しい生物的知見を生み出すことに大きく貢献することが期待できます。


社会数理モデル学
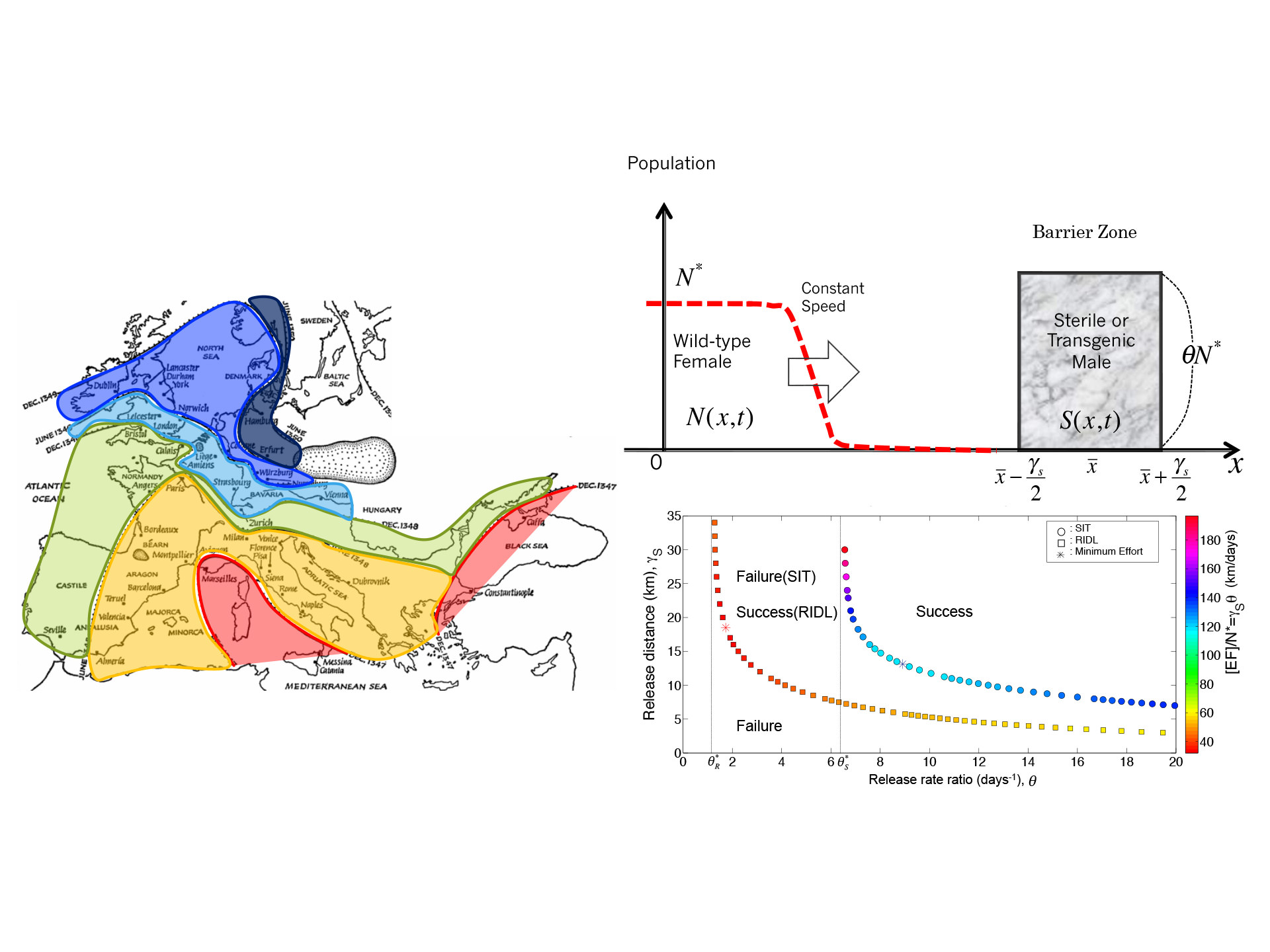
伝染病の広がりを防ぐ最適時空間戦略
Infectious diseases such as malaria and dengue fever are not transmitted directly from person to person, but are spread through mosquitoes. Reducing (eradicating) the number of mosquitoes is a fundamental policy to prevent the spread of infectious diseases, but this requires a huge amount of taxpayers' money. This study considers what policies are economically effective to control vector-borne epidemics. We aim to develop a approach is highly versatile in its application to a variety of epidemics, and we are attempting to apply it to the study of effective control policies for a variety of epidemics.
マラリアやデング熱などの伝染病は、人から人へ直接に感染するのではなく、蚊を媒介して人間社会に広まります。そして、その蚊の数を減らす(根絶する)事が伝染病の広がりを止められる根本的な政策になりますが、そのためには莫大な税金が必要になります。本研究では、このような昆虫媒介の伝染病が空間的に広がっている時に、どのような政策を使う事が経済的かつ有効であるかと考察しています。この研究手法は、様々な伝染病における応用汎用性が高く、様々な伝染病の空間的コントロール政策研究への応用を試みています。

都心に広がる空き家問題の数理モデルと最適政策
With the decline in population, the problem of empty houses, Akiya, is becoming more serious in Japan today, not only in the suburbs but also in the cities. This study builds a mathematical model and examines what kind of government policies would be effective to solve this problem.
人口減少に伴い、今の日本では郊外のみならず、都会でも空き家の問題は深刻になっています。本研究では、この問題を解決するためにどのような政策が有効なのか、数理モデルを構築し、考察しています。