研究内容 Research Topics

粒子法の数学解析と工学・防災への応用Numerical analysis of particle methods and application into engineering and disaster science

研究の背景・目的

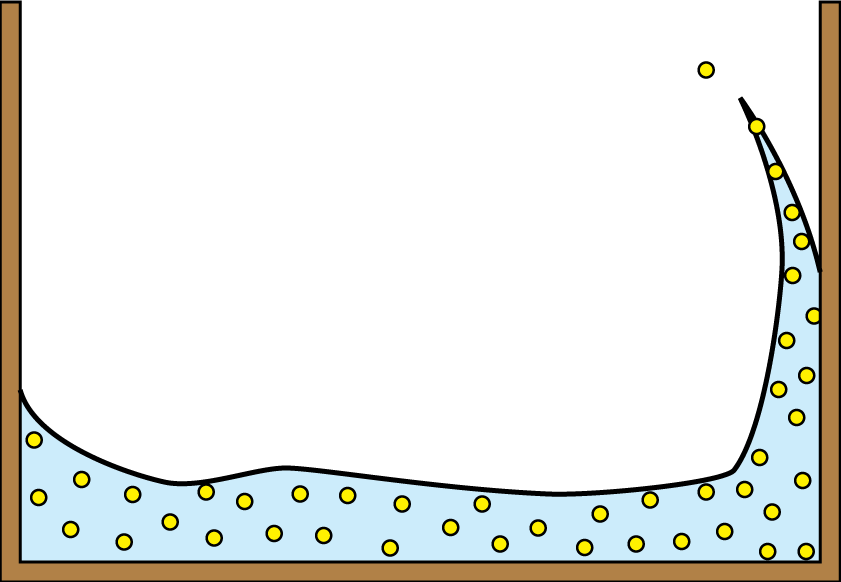
粒子法は物理現象を計算機でシミュレーションするときに用いられる計算手法（離散化手法）の１つで、物体を表現する点の集合が物体の粒子のように時間の経過とともに移動することが特徴です。粒子の移動によって領域の形状変化を容易に表現できることから、粒子法は津波やビルの破壊のような領域が激しく変形・分離・結合するような物理現象のシミュレーションに幅広く用いられています。粒子法は1970年代後半に開発された計算手法で、古くから利用されてきた差分法や有限体積法を一般化した計算手法としても捉えることができます。そのため、従来の計算手法より適用可能な範囲が広いという意味で汎用性に優れています。

しかし、汎用性が高い一方で、粒子法の計算結果の精度や安定性が十分でないという問題があり、さまざまな粒子法の改良の研究がなされてきました。そこで、本研究では粒子法を数学的側面から研究を行うことで、粒子法のより深い理解やシミュレーション結果の信頼性の向上に貢献することを目指します。

粒子法の数学解析

粒子法の数学解析は、これまでわずかに先行研究はあったものの、実際にシミュレーションで利用されている粒子法に直接貢献できるものはありませんでした。そこで我々は離散化パラメータの正則性や粒子分布の接続性といった新たな条件を導入することで粒子法の打ち切り誤差評価や安定性評価などを数学的に厳密に証明しました。本研究により粒子法の精度や安定性のような信頼性が（一部）担保されただけでなく、従来はトライ＆エラーで定めていたパラメータの決定方法の指針を示したことになります。その他にも、粒子法の改良手法などを数学的に矛盾なく導出・解析することで改良手法を新たな視点で理論的に解釈する試みも行っています。

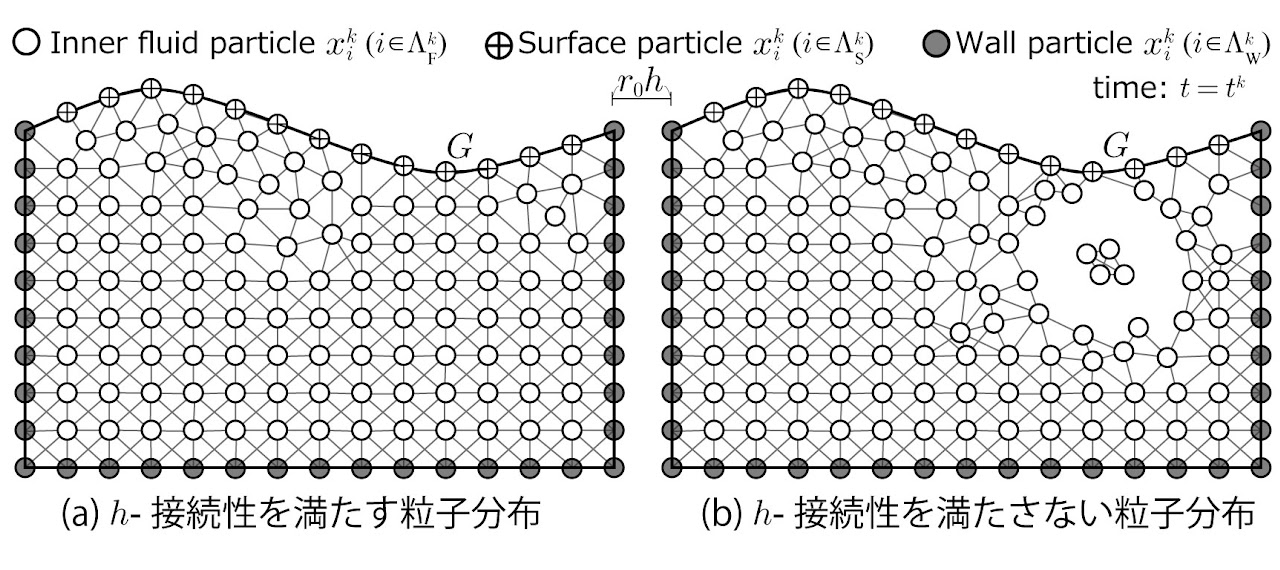
粒子法に対する数学解析の応用

本研究では、粒子法の数学解析で得られた知見を用いて粒子法の精度や安定性の改善を目指します。例えば、誤差評価で得られた誤差の上限を構成するパラメータを観察することでより良いパラメータ選択を行ったり、安定性の具体的な制約条件をより満足するように計算手順を修正することで従来手法の改良を行っています。また、より複雑な現象の高精度なシミュレーションに向けて、数学的には厳密に解析することは難しいものの、最新の数学的な知見を応用することで、最先端のシミュレーションに対して信頼性を向上させる取り組みも行っています。

超双対数の理論拡張と計算力学への応用Theory and application of hyper-dual numbers

研究の背景・目的

双対数（二重数、Dual number）とは二乗して零となる仮想的な数で、微分可能な関数を双対数の空間に拡張すると、関数の１階微分を双対数の係数を用いて厳密に表現することができます。この双対数を高次に拡張したものが超双対数（Hyper-dual numbers）で、関数の高階微分を超双対数の係数を用いて厳密に表現することができます。この性質を応用して、超双対数は高精度な高階微分の数値計算に応用されています。

超双対数の理論拡張

超双対数による微分の数値計算は、従来の微分の数値計算手法（例えば自動微分）よりも、演算規則が単純であり、多変数関数の偏微分にも拡張が容易であることが特徴です。しかしながら、数学的な拡張は容易であるものの、その演算規則の実装は微分階数が増えるにつれて非常に複雑になることから、高階微分への応用は現状では限られています。また、応用できる関数も限られています。そこで、本研究では超双対数を具体的な応用を見据えて理論的拡張することを目的としています。現在までに、超双対数の行列表示を導入することで、超双対数の演算規則を行列の演算に置き換えることができ、実装の簡略化および計算の高速化に成功しています。また、行列の固有値や固有ベクトルの高階微分へ計算手法を拡張しています。

高次元統計学に基づくシングルセル遺伝子発現データのノイズ削減Noise reduction of single-cell gene expression data based on high-dimensional statistics

研究の背景・目的

シングルセル遺伝子発現解析（scRNA-seq）とは、１細胞ごとのすべてのRNA発現量をデータ化する実験技術で、そのデータはシングルセル遺伝子発現データと呼ばれます。現在、１度の実験で数百～数万細胞・数万遺伝子の遺伝子発現量のデータが取得できます（非負整数行列データ）。シングルセル遺伝子発現データは非常に多くの細胞の遺伝子情報を有しているため、そのデータ解析によって未知の細胞種の発見や細胞分化の構造の理解が期待されています。

しかし、現在のシングルセル遺伝子発現解析では検出率が非常に低く（平均10％程度）、検出率のばらつきによるノイズ（ランダムサンプリングノイズ）が発生します。さらに、シングルセル遺伝子発現データは次元（遺伝子数）が非常に高いため、距離や統計量の計算でノイズが蓄積することで真の構造が得られない次元の呪いが発生します。次元の呪いはほとんど全てのデータ解析手法に悪影響を及ぼすため、現在のシングルセル遺伝子発現データ解析では真の１細胞の情報を取得できない問題がありました。

本研究では、高次元統計学に基づいて、シングルセル遺伝子発現データの次元の呪いを解決する手法を開発することを目的とします。

高次元データのノイズ削減手法 RECODE の開発

本研究では高次元統計学に基づくノイズ削減手法RECODEを開発しました。RECODEはデータの分散に基づいて、真の情報とノイズを分離し、ノイズのみを取り除く手法で、ノイズの分散が推定可能なデータに適用できます。さらに、本研究ではシングルセル遺伝子発現データのノイズ（ランダムサンプリングノイズ）の分散を理論的に導き、RECODEでシングルセル遺伝子発現データのノイズを削減することに成功しました。また、エピゲノムデータ（scATAC-seq data）などへの拡張も進めています。

超高次元トポロジカルデータ解析手法の開発と
位相的細胞分化構造解析Development of ultra-high-dimensional topological data analysis method and topological cell differentiation structure analysis

研究の背景・目的

細胞が外部からの刺激などによって新たな機能を持つ細胞へ変化することを細胞分化と呼びます。細胞分化の過程では、細胞は遺伝子の働き（発現量、RNAやタンパク質の合成量）を変化させながら、様々な細胞状態を経由して複数の細胞へ変化します。そのような細胞分化の分岐構造を解析することは細胞分化を細胞集団・単一細胞で予測・制御することに役立ち、疾患治療・創薬・予防（免疫）の研究発展や臨床応用が期待できます。

細胞分化を誘導する遺伝子は数千～数万種（ヒトは約20,000種）存在するため、細胞集団の分化構造は超高次元空間に潜むトポロジー構造（ループや枝分かれ） と考えることができます。しかしながら、従来のデータ解析手法では高次元トポロジー構造を容易に抽出できないことから、細胞分化の詳細な構造を抽出することができません。そこで、本研究では細胞分化構造の抽出に特化したトポロジカルデータ解析手法を開発し、細胞分化構造を理解することを目的とします。

細胞分化構造のためのトポロジカルデータ解析手法の開発

トポロジカルデータ解析手法”Mapper”は高次元データが持つトポロジー構造を保ちながらデータ圧縮する手法です。一方で、遺伝子データのような超高次元データの場合に、わずかな観測誤差の影響を受けやすく（次元の呪い）、本来のトポロジー構造を抽出することができないといった問題があります。また、複数の分岐構造が重なりあう地点の分岐情報が圧縮されてしまうという問題があります。そこで、高次元統計学およびトポロジー解析に基づいて細胞分化構造に特化したトポロジカルデータ解析手法を開発しています。

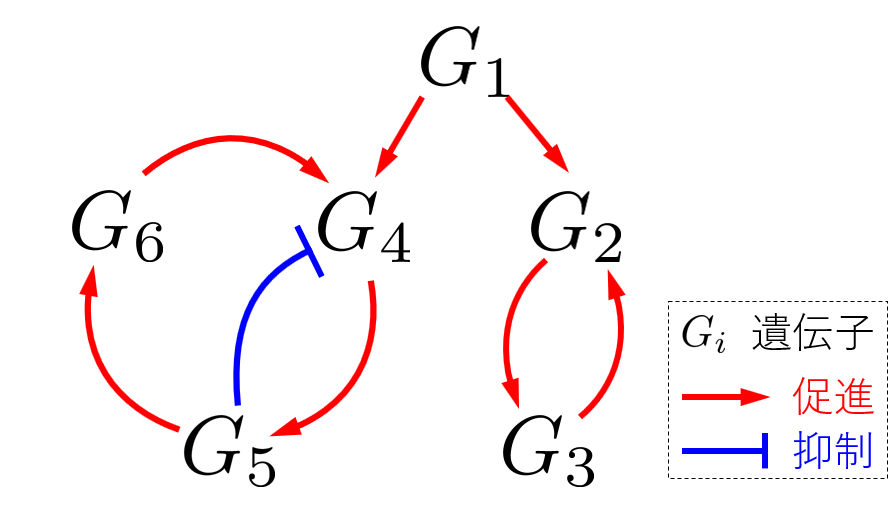
統計的因果探索による遺伝子制御ネットワーク構造の理解Understanding gene regulatory network structure by statistical causal search

研究の背景・目的

上記の細胞分化構造の理解は細胞集団（マクロ）での時間変化を取り扱うことには適していますが、単一細胞（ミクロ）な時間変化を取り扱うことはできません。したがって、より詳細な分化構造を理解・制御するためには、単一細胞レベルの詳細な構造、つまり細胞内の遺伝子の働き（発現の変化）を理解することが必要です。遺伝子発現現象は遺伝子が互いに発現を直接的に促進・抑制（転写制御）することが知られています。その制御の相互作用をネットワークとして表現したものを遺伝子制御ネットワークと呼びます。遺伝子制御ネットワークは遺伝情報だけでは説明できない生物の多様性を表現する要因の一つと考えられています。

本研究では、転写制御を含む遺伝子発現現象の数理モデルとネットワーク推定（統計的因果探索）に基づいて、遺伝子発現データから遺伝子制御ネットワークを推定手法を開発することで、単一細胞レベルでの細胞分化構造を理解することを目的とします。

遺伝子制御ネットワーク手法の開発

本研究では10X Genomicsに代表される近年主流な単一細胞遺伝子発現解析（scRNA-seq）で収集可能な、少タイムポイント（数個～数十個）・多サンプル（数百～数千）の単一細胞の遺伝子発現データを対象とします。このようなデータの場合、従来の数理モデルのパラメータ推定に基づくネットワーク推定ではタイムポイントの不足によって良い推定ができません。そこで、本研究では時間情報を利用せずに、データの分布を解析することで因果情報を抽出できる統計的因果探索手法のLiNGAM（リンガム）に着目しました。本研究ではLiNGAMで仮定する数理モデルを遺伝子発現現象を表す数理モデル（非線形力学システム）へ拡張することに成功し、遺伝子発現データから遺伝子制御ネットワークを推定する手法を開発しました。本手法は遺伝子制御ネットワークの制御の種類（促進・抑制）も推定できます。