速度を持つ高次元データの位相的データ解析超双対数に基づく固有系の微分高階微分計算のための超双対数の行列表現とその基本定理非圧縮性Navier–Stokes方程式に対する陽的粒子法の収束性検証と重み関数の最適化陰的SPH法を用いた高粘性流体シミュレーションの改良ISPH法の一意可解性および安定性解析離散SobolevノルムによるPoisson方程式に対する一般加粒子法の一意可解性および安定性安定化ISPH法の理論的解釈Voronoi分割に基づく一般化粒子法の近似微分作用素の打ち切り誤差評価Voronoi分割に基づく一般化粒子法の補完作用素の打ち切り誤差評価安定化ISPH法による拡張ダルシー則とナビエ・ストークス方程式の統一解法
速度を持つ高次元データの位相的データ解析V-Mapper: topological data analysis for high-dimensional data with velocity
| 著者 | Yusuke Imoto*, Yasuaki Hiraoka. |
|---|---|
| 出版年月日 | 2023年4月1日 |
| 掲載雑誌 | Nonlinear Theory and Its Applications, IEICE, Vol. 14 |
| アクセス | ジャーナル |
| ページ数 | 13 |
| 抄録 | 近年、1細胞遺伝子発現データのようなビッグデータがさまざまな分野で取得できるようになりました。しかし、そのようなビッグデータから分析者が必要とする情報をデータ解析で抽出することは容易ではなく、抽出したい構造を数学的に記述し、その構造を出力できるデータ解析手法を適切に設計する必要があります。今世紀になって、数学分野の一つであるトポロジーの理論に基づいてデータの「かたち」を抽出することができるトポロジカルデータ解析が実用化され、さまざまな分野で応用されています。生命科学においては、トポロジカルデータ解析手法のMapper(マッパー)を1細胞遺伝子発現データに応用することで、細胞分化の経路構造を表す「かたち」を抽出する研究が行われてきました。しかし、Mapperは細胞分化の「かたち」を可視化できるものの、細胞分化の進展方向を表す「ながれ」を抽出できないことが問題でした。 そこで、本研究ではMapperと遺伝子発現量の時間変化を抽出できるRNA velocity法に着目し、細胞分化の「かたち」と「ながれ」を同時に抽出できるトポロジカルデータ解析手法V-Mapper(velocity Mapper)を開発しました。V-Mapperは空間内の点集合とその上の流れ場を入力とし、Mapperの出力であるグラフ構造に流れ場を埋め込むことで、データの「かたち」と「ながれ」を重み付き有向グラフ(V-Mapperグラフ)によって可視化することができます。さらに、V-Mapperグラフにグラフホッジ分解を適用することで、複雑な流れ構造から大域的な流れ構造を表すグラフ上の勾配流を抽出することができます。本研究ではV-Mapperをマウス膵臓内分泌細胞の1細胞遺伝子発現データに適用し、分化後期に現れる複数の内分泌細胞への複雑な分化構造を抽出することに成功しました。本成果により、可塑性や周期性のようなトポロジカルな特性を含む細胞分化経路を抽出することが可能になります。V-Mapperを用いた1細胞遺伝子発現データ解析により、細胞分化メカニズムの解明に貢献することができ、再生医療における分化誘導の効率化など、臨床応用の進歩を強力に後押しすることが期待されます。 |
超双対数に基づく固有系の微分Hyper-dual number-based numerical differentiation of eigensystems
| 著者 | Masaki Fujikawa*, Masato Tanaka, Naoto Mitsume, Yusuke Imoto*. |
|---|---|
| 出版年月日 | 2022年2月15日 |
| 掲載雑誌 | Computer Methods in Applied Mechanics and Engineering, Vol. 390 |
| アクセス | ジャーナル |
| ページ数 | 21 |
| 抄録 | 複合材料の変形シミュレーションに現れる固有値の高階微分の高精度計算手法開発に関する論文です。 具体的な目的は3×3行列Aの固有値の冪乗和(f(A)=λ_1^a+λ_2^a+λ_3^a, a:実数)に対する高階偏微分(最大4階偏微分、微分変数は行列の成分A_ij)を高精度に計算することで、これを超双対数(Hyper-dual numbers)という冪零性を持つ代数的対象を用いて開発したものです。 特に、固有値が重解のときにf(A)の微分は存在するが、重解の固有値λ_iの微分は存在しないという困難性がありますが、これを行列のlog/exp級数展開と超双対数を組み合わせることで計算可能にしたところが面白い点です。 |
高階微分計算のための超双対数の
行列表現とその基本定理Fundamental theorem of matrix representations of hyper-dual numbers for computing higher-order derivatives
| 著者 | Yusuke Imoto, Naoya Yamanaka, Takeo Uramoto, Masato Tanaka, Masaki Fujikawa, Naoto Mitsume. |
|---|---|
| 出版年月日 | 2020年6月1日 |
| 掲載雑誌 | JSIAM Letters, Vol. 12, pp. 29–32 |
| アクセス | ジャーナル(オープンアクセス) |
| ページ数 | 4 |
| 抄録 | 本論文は仮想的な数体系である超双対数(hyper-dual numbers, HDN)を行列で表すことで、効率的な多変数や高階の微分の計算手法を提案しています。 超双対数は2乗が0となる仮想的な複数の元を用いた数で、超双対数上の関数をテイラー展開に基づいて定義することで、微分法則(和・積・合成関数の微分公式)を全て保存する体系となります。 しかしながら、超双対数の演算は直感的であるものの、計算の実装が難しいという欠点がありました。そこで、本研究では超双対数の基本元を行列で表すことで、超双対数の演算規則を全て行列の演算(行列の和と積)に置き換えることに成功しています。 これは、全ての微分法則は行列の演算で表現できることを表しており、それを定理で示しています。本研究は現在主流である微分計算手法の自動微分に換わる新しい技術になることが期待できます。 |
非圧縮性Navier–Stokes方程式に対する
陽的粒子法の収束性検証と重み関数の最適化Convergence study and optimal weight functions of an explicit particle method for the incompressible Navier–Stokes equations
| 著者 | Yusuke Imoto, Satori Tsuzuki and Daisuke Nishiura |
|---|---|
| 出版年月日 | 2019年9月18日 |
| 掲載雑誌 | Computational Particle Mechanics, Vol. 6 (4), pp. 671–694 |
| アクセス | ジャーナル(会員のみ),プレプリント(オープンアクセス) |
| ページ数 | 24 |
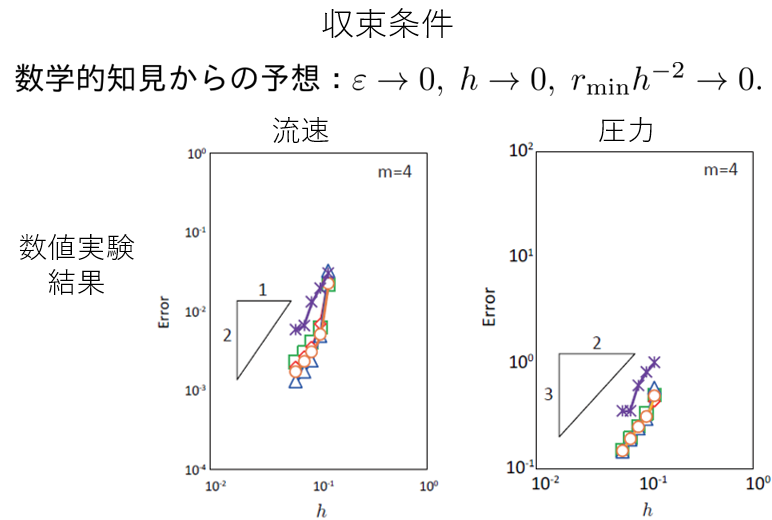
| 抄録 | 本論文は工学への応用論文である.非圧縮性Navier-Stokes方程式に対する陽的解法に基づく粒子法は津波シミュレーションのような自由表面を含む問題に広く用いられている。 しかしながら,陽的粒子法の近似解が収束するための条件は数学的にも数値実験的にも明らかになっていない。 そこで本論文では,数学的な手順で導出された陽的粒子法を提案し,空間離散化における打ち切り誤差評価を行うことで提案手法の収束性の十分条件を予想し,近似解が収束することを数値実験によって検証した(左下図)。 次に,提案手法の精度を向上するために,打ち切り誤差評価における誤差の係数を最小化する最適な重み関数を導出し,悪条件下でもロバストに精度を維持できることを数値実験によって確認した。 最後に,自由表面を含む問題に応用するために,自由表面付近でも安定に計算できる修正を提案し,水柱崩壊(ダムブレイク)問題で安定かつ実験値に近い圧力分布が得られることを確認した(右下図)。 |
陰的SPH法を用いた高粘性流体シミュレーションの改良Improvements in highly viscous fluid simulation using a fully implicit SPH method
| 著者 | Daniel Morikawa, Mitsuteru Asai, Nur’Ain Idris, Yusuke Imoto and Masaharu Isshiki |
|---|---|
| 出版年月日 | 2019年9月18日 |
| 掲載雑誌 | Computational Particle Mechanics, Vol. 6 (4), pp. 529–544 |
| ページ数 | 16 |
| アクセス | ジャーナル(会員のみ) |
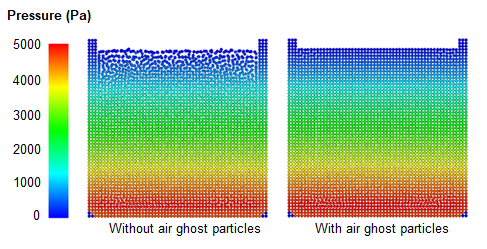
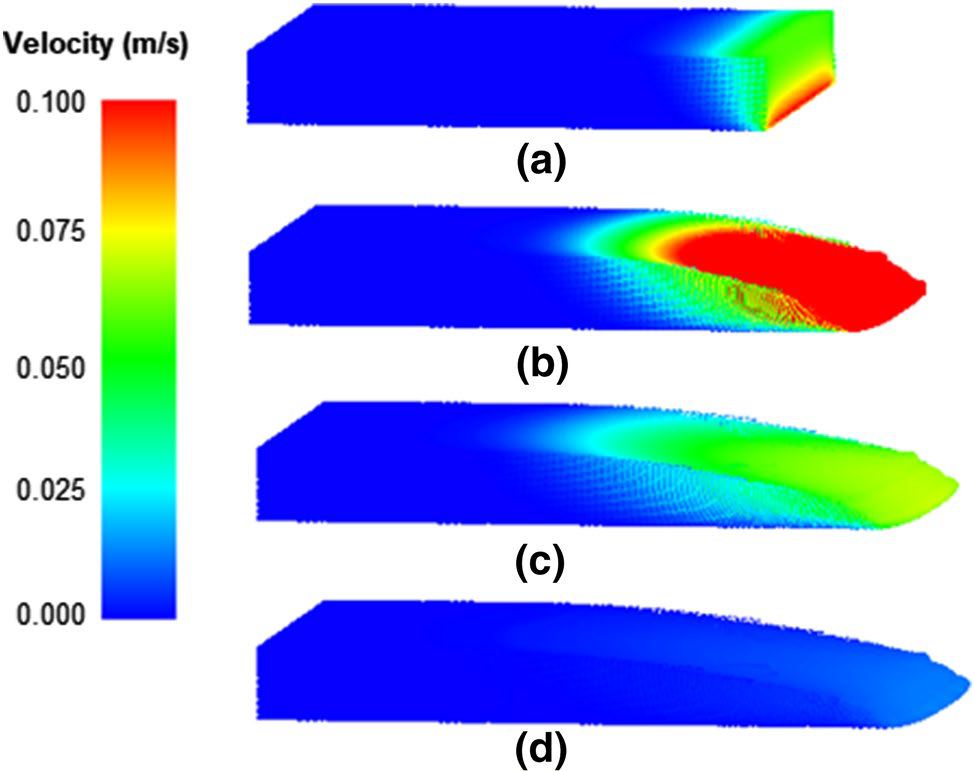
| 抄録 | 本論文では,粒子法の一種であるSPH法を用いた自由表面を含む高粘性流れ問題に対する数値計算手法を提案する。 提案手法の特徴は「完全陰解法のSPH法である」「自由表面の離散化に高解像度の仮想粒子モデルを用いていること」である。 自由表面を含む流れ問題の場合,領域形状が時間の変化とともに複雑に変形するため,領域形状の変化に合わせて解析点を移動させる粒子法が有効である。 そのため,本論文では非圧縮性(低粘性)流れ問題で幅広く用いられている粒子法である安定化ISPH法を採用した。 しかしながら,従来の半陰解法の安定化ISPH法では予測式を陽的に解くことで現れる時間刻みの条件が,高粘性流体の場合に支配的となるため,本論文では予測式も陰的に解く完全陰解法の安定化ISPH法を導入した。 また,自由表面の形状変化が伴う高粘性流れ問題の場合,形状の変化が内部の流れに大きく影響する(自由表面の変化が支配的な問題となる)ため,自由表面付近の高精度化が重要となる。 そのため,自由表面付近の粒子数不足による精度低下を緩和する高解像度の仮想粒子モデル(SPPモデル)を導入した.以上の修正の下で,静水圧(右上図)および水柱崩壊(右中央図)の数値実験を行い,安定した自由表面形状が得られること,実用的な範囲の時間刻みで精度良い解が得られることを定性的に確認した。 さらに,高粘性流体の落下・接触・結合を表現する複雑問題であるコイリング現象(右下図)の数値実験を行い,流体がうねりながら巻き付く現象を再現することができた. *本論文のコイリング現象の数値実験動画は第23回計算工学講演会(2018年)のグラフィクスアワードで最優秀賞を受賞しています [link] |

ISPH法の一意可解性および安定性解析Unique solvability and stability analysis for incompressible smoothed particle hydrodynamics method
| 著者 | Yusuke Imoto |
|---|---|
| 出版年月日 | 2019年3月23日 |
| 掲載雑誌 | Computational Particle Mechanics, Vol. 6 (2), pp. 297–309 |
| ページ数 | 13 |
| アクセス | ジャーナル (会員のみ),プレプリント(オープンアクセス) |
| 抄録 | ISPH法は非圧縮性Navier-Stokes方程式の空間方向にSPH法,時間方向に射影法を適用した粒子法の一種で,津波遡上シミュレーションを目的とした低粘性の激しい流れ問題や,高粘性流体や非ニュートン流体の流れ問題などに利用されている。 本論文では離散化パラメータに対する3つの条件:h-接続性,準正則性,時間刻みの制約条件を導入し,ISPH法における自由表面を含む半陰的および陰的スキームに対して,数学的な一意可解性(2-3次元)および流速の安定性(2次元)の証明を行った。 本解析により,ISPH法における安定な計算を行うための一部の離散化パラメータの具体的な決定方法が明らかになった。 また,本論文内のRemarkにおいて,それらの離散化パラメータの条件が経験則とよく一致しており,十分実用的な範囲であることを確認している。 *本論文はSPH法のワーキング・グループ”SPHeric”の”Grand Challenge #1 Convergence, consistency and stability”における”list of relevant key publications”内で紹介されています [link] *本研究に関する講演で2018年度日本数学会応用数学研究奨励賞を受賞しています [link] |

離散SobolevノルムによるPoisson方程式に対する
一般加粒子法の一意可解性および安定性Unique solvability and stability of a generalized particle method for a Poisson equation in discrete Sobolev norms
| 著者 | Yusuke Imoto |
|---|---|
| 出版年月日 | 2019年2月14日 |
| 掲載雑誌 | Applications of Mathematics, Vol. 64 (1),pp. 33–43 |
| ページ数 | 11 |
| アクセス | ジャーナル(会員のみ),プレプリント(オープンアクセス) |
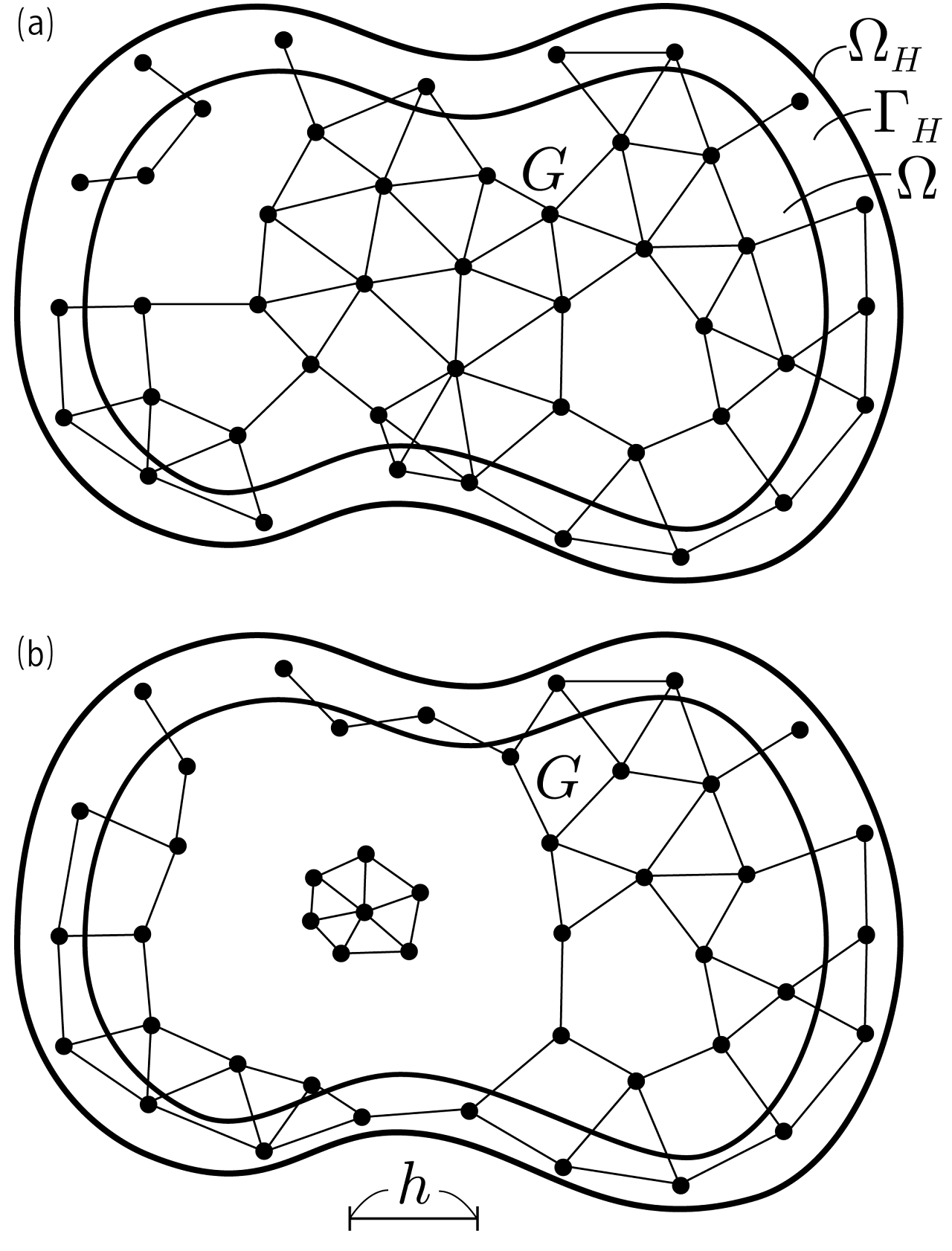
| 抄録 | 本論文は実際の流れ問題への応用を想定した粒子法で離散化されたPoisson方程式に対して一意可解性および安定性を証明したものである。 Poisson方程式は,非圧縮性流れ問題の射影法に基づく離散化で現れる圧力Poisson方程式に対応した生成項が発散で表されるものを導入し,SPHやMPS法のような従来の粒子法を統一的に扱うことができる一般加粒子法で離散化されたものを考える。 この離散方程式に対して,h接続性と呼ばれる粒子分布と影響半径の関係性に対する制約条件を導入し,h接続性のもとで一意可解性を示した。 次に,離散空間における部分積分のような性質を満たすように,粒子法における離散Sobolevノルムを導入し,いくらかの補題を示すことで離散方程式の安定性を示した。 本論文では,実際の粒子法でも経験的に用いられている,粒子間の相互作用が差分でない発散作用素を用いているが,この発散作用素は有限体積法の発散近似の拡張で導出できることを付録で示している. *本研究に関する講演で日本応用数理学会 2018年研究部会連合発表会優秀講演賞を受賞しています [link] |
安定化ISPH法の理論的解釈
ー エネルギー最小化問題からの安定化項の導出 ー
| 著者 | 井元佑介,浅井光輝 |
|---|---|
| 出版年月日 | 2019年1月31日 |
| 掲載雑誌 | 土木学会論文集A2(応用力学), 74巻2号, pp. 159–166 |
| ページ数 | 8 |
| アクセス | ジャーナル(会員のみ) |
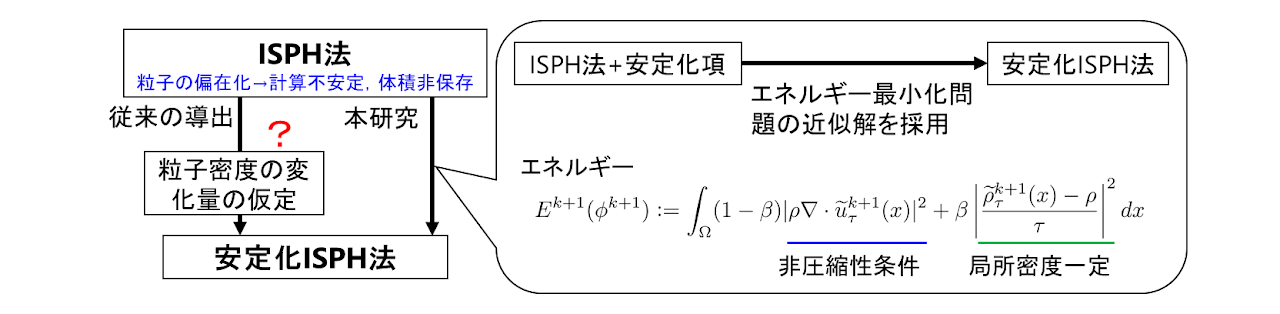
| 抄録 | 安定化ISPH法は非圧縮性Navier-Stokes方程式に対する粒子法の一種で,通常のISPH法における安定化項を付加した安定化手法である。 しかし,安定化項が粒子の偏在化を防ぐ寄与があるかどうかがこれまでの導出からは不明瞭であった。 本論文では非圧縮性の条件と粒子の均一性の誤差に関するエネルギーを導入し,そのエネルギーを最小化することで安定化ISPH法を導出した。 本導出により,安定化ISPH法は非圧縮性の条件と粒子密度一定の条件を重み付きで満たすように制約を与えた手法であると解釈することができる。 さらに,エネルギー最小化問題の真の解と近似解の誤差から,安定化項に用いる安定化係数が1より十分小さい正の実数であることを示し,数値実験の経験則と一致することを述べた。 本導出に基づけば,関連する安定化手法における安定化項の統一的な理解・導出につながり,今後新たな安定な数値解法を構成する際の重要な方法論となり得ることが期待できる。 |
Voronoi分割に基づく一般化粒子法の
近似微分作用素の打ち切り誤差評価Truncation error estimates of approximate differential operators of a particle method based on the Voronoi decomposition
| 著者 | Yusuke Imoto and Daisuke Tagami |
|---|---|
| 出版年月日 | 2017年10月19日 |
| 掲載雑誌 | JSIAM Letters, Vol. 9, pp. 69–72 |
| ページ数 | 4 |
| アクセス | ジャーナル(オープンアクセス) |
| 抄録 | 本論文ではImoto–Tagami(2016)の拡張として,粒子法で用いられている1階と2階の微分作用素に対して打ち切り誤差評価を行った。 SPHやMPSのような従来の粒子法で用いられている微分作用素を一般的に記述する一般化勾配作用素および一般化ラプラス作用素を導入し,粒子体積をボロノイ分割の各ボロノイ領域の体積とした微分作用素を考える。 そして,ボロノイ領域の最大半径で定義される粒子分布の指標を導入し,その指標と影響半径で定義される離散化パラメータの正則性を導入した。 その正則性と重み関数に対するいくらかの条件のもとで一般化勾配作用素および一般化ラプラス作用素の打ち切り誤差評価を示した。 さらに,対応する数値実験を実施し,定理で得られた収束次数とよく一致した結果が得られることを確認した. |
Voronoi分割に基づく一般化粒子法の
補完作用素の打ち切り誤差評価A truncation error estimate of the interpolant of a particle method based on the Voronoi decomposition
| 著者 | Yusuke Imoto and Daisuke Tagami |
|---|---|
| 出版年月日 | 2016年5月21日 |
| 掲載雑誌 | JSIAM Letters, Vol. 8, pp. 29–32 |
| ページ数 | 4 |
| アクセス | ジャーナル(オープンアクセス) |
| 抄録 | 本論文はSPHのような粒子法で用いられている補間作用素に対して打ち切り誤差評価を行った。 本論文では粒子体積をボロノイ分割の各ボロノイ領域の体積とした補間作用素を考える。 ボロノイ領域の最大半径で定義される粒子分布の指標を導入し,その指標と影響半径で定義される離散化パラメータの正則性を導入した。 その正則性と重み関数に対するいくらかの条件のもとで補間作用素の打ち切り誤差評価を示し,対応する数値実験を実施し,定理で得られた収束次数とよく一致した結果が得られることを確認した。 |
安定化ISPH法による拡張ダルシー則と
ナビエ・ストークス方程式の統一解法
| 著者 | 森本敏弘,浅井光輝,笠間清伸,藤澤和謙,井元佑介 |
|---|---|
| 出版年月日 | 2015年2月20日 |
| 掲載雑誌 | 土木学会論文集 A2 (応用力学), 70巻2号, pp. 213–221 |
| ページ数 | 9 |
| アクセス | ジャーナル(オープンアクセス) |
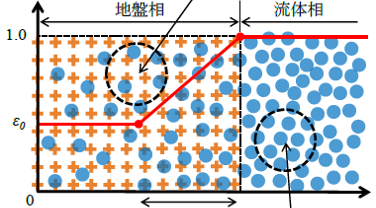
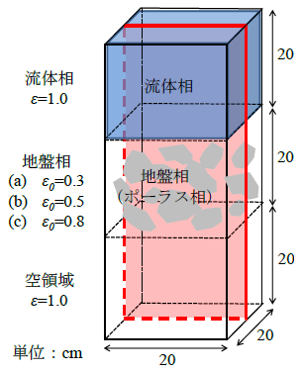
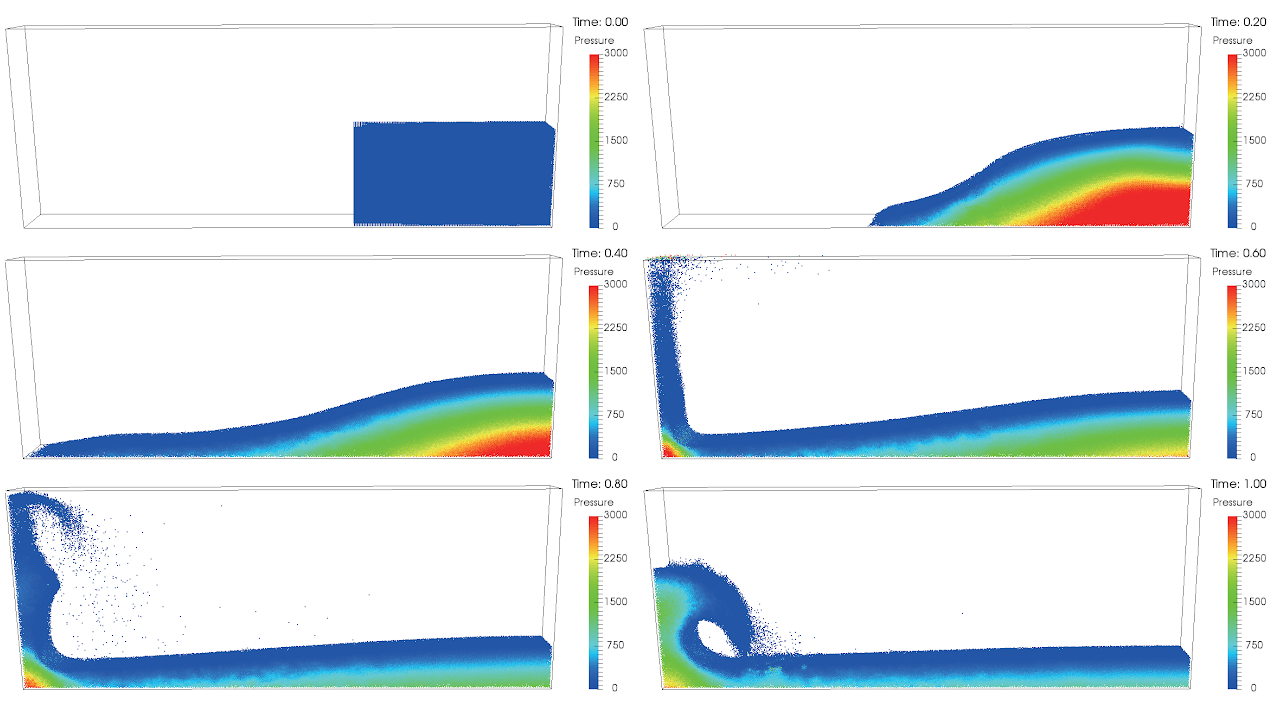
| 抄録 | 浸透流による防波堤の崩壊現象の解明するために,本論文では粒子法を用いた地表流と浸透流の統一的な数値計算手法を提案する。 支配方程式として非圧縮性Navier-Stokes方程式と拡張Darcy則を間隙率εを用いて統一的に記述した統一方程式を採用し,非圧縮性Navier-Stokes方程式に対する粒子法の一種である安定化ISPH法をその方程式に拡張した。 本拡張においては,「問1:統一方程式をどのように離散化するか」「問2:地表流と浸透流内の粒子密度およびそれらの遷移方法をどのように定義するか?」が重要な問いである。 問1は射影法に基づいて運動方程式を予測式と修正式に分離し,修正式と連続の式を用いて圧力Poisson方程式を導入する。ここで,安定化ISPH法に基づき,圧力Poisson方程式には粒子密度に関する安定化項を付加する.ただし,安定化項に用いる粒子密度は地盤内では未定義のため問2が問題として浮上する。 問2は浸透流の領域(地盤相)のバックグラウンドマーカーを配置し,影響半径内にある地盤マーカーの密度によって間隙率εを定義し,浸透流内の粒子密度はε倍することによって定義した(右上図)。 本定義により,間隙率は地盤相および流体相の境界付近でも連続的に変化するので計算が安定となる。 さらに,地盤相(ポーラス相)を通過する流体の落下問題(右下)の数値実験を行い,体積変化,圧力分布,落下速度をを確認することで提案手法の定性的な妥当性を確認した。 |