Research Overview
Establishing a Fusion-Based Approach Linking Morphology to Medicine and Human Biology
— From Understanding Pattern Formation in Life to Elucidating Diseases and Advancing Therapeutic Applications —
In recent years, interdisciplinary research that leverages the power of mathematics to address complex phenomena and challenges has advanced rapidly, transforming the landscape of science, medicine, and society. At the forefront of this paradigm shift, our research group is engaged in a distinctive exploration of applied mathematical science—particularly in the areas of mathematical medicine, immunology, and biology—approached through the conceptual lenses of patterns and morphology.
We aim to unravel fundamental questions such as “How are humans formed?” and to address challenging clinical issues like autoimmune diseases by integrating both model-driven and data-driven approaches. By combining these complementary methodologies, we are forging new pathways to understanding biological and medical systems.
In clinical medicine, where biological experimentation is often difficult and conventional approaches offer limited solutions, we construct mathematical models grounded in unconventional perspectives. These models are developed in close synergy with clinical data, biological experimentation, AI-based data science, and mathematical analysis—enabling the creation of novel and effective research frameworks. Guided by the central themes of patterns and morphology, our goal is to reveal the underlying principles that govern biological phenomena and to generate new conceptual frameworks for understanding cellular function. These insights are translated into applications for regenerative medicine and therapeutic innovation. Moreover, through the development and application of mathematical models, we seek to uncover universal principles of life and gain deeper insight into the essence of human biology. In doing so, we are pioneering emerging fields such as mathematical human biology, spatial mathematical immunology, and mathematical medicine.
Publications
Seirin-Lee, S^., & Kimura, A^. (2025). Geometric factors for cell arrangement: How do cells determine their position in vivo? Seminars in Cell & Developmental Biology, 169, 103604. https://doi.org/10.1016/j.semcdb.2025.103604
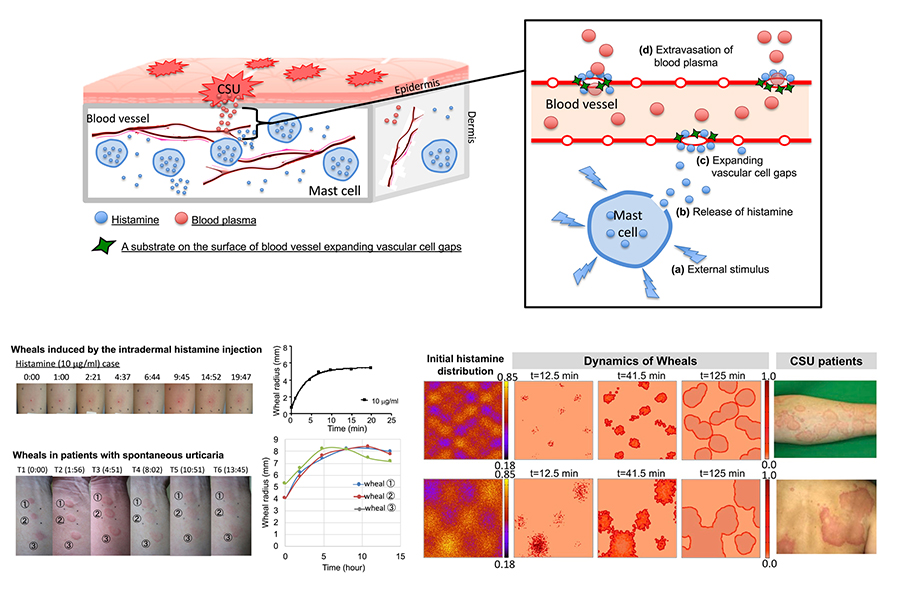
Seirin-Lee, S^., Takahagi, S., & Hide, M^. (2025). Pathophysiological mechanisms of the onset, development, and disappearance phases of skin eruptions in chronic spontaneous urticaria. Bulletin of Mathematical Biology, 87(1). https://link.springer.com/article/10.1007/s11538-024-01380-3
Seirin-Lee, S^., Matsubara, D., Yanase, Y., Kunieda, T., Takahagi, S^., & Hide, M. (2023). Mathematical-based morphological classification of skin eruptions corresponding to the pathophysiological state of chronic spontaneous urticaria. Communications Medicine, 3, 171. https://doi.org/10.1038/s43856-023-00404-8
Seirin-Lee, S^., Yamamoto, K., & Kimura, A^. (2022). The extra-embryonic space and the local contour are critical geometric constraints regulating cell arrangement. Development, 149, dev200401. https://doi.org/10.1242/dev.200401
Seirin-Lee, S. (2021). The role of cytoplasmic MEX-5/6 polarity in asymmetric cell division. Bulletin of Mathematical Biology, 83, 29. https://doi.org/10.1007/s11538-021-00860-0
Seirin-Lee, S., Yanase, Y., Takahagi, S., & Hide, M. (2020). Multifarious eruptions of urticaria solved by a simple mathematical equation. PLOS Computational Biology, 16(1), e1007590. https://doi.org/10.1371/journal.pcbi.1007590
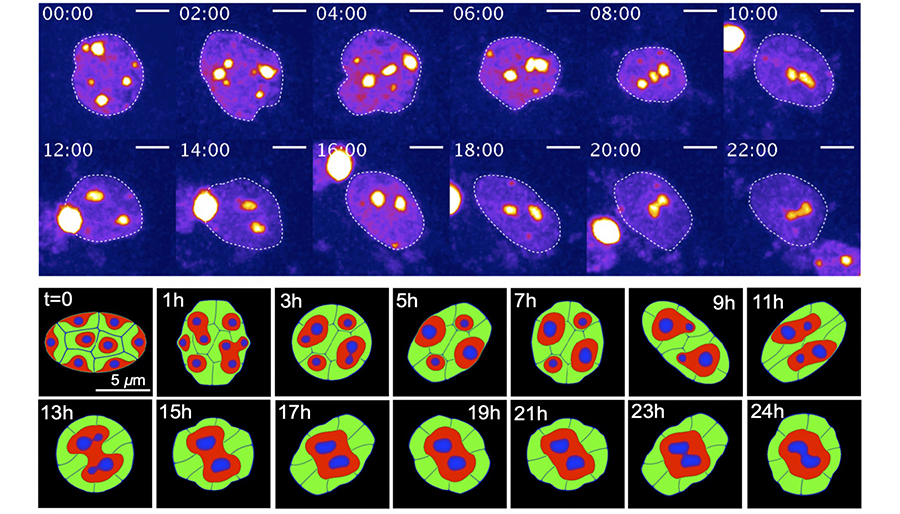
Seirin-Lee, S., Osakada, F., Takeda, J., Tashiro, S., Kobayashi, R., Yamamoto, T., & Ochiai, H. (2019). Role of dynamic nuclear deformation on genomic architecture reorganization. PLOS Computational Biology, 15(8), e1007289. https://doi.org/10.1371/journal.pcbi.1007289
Kuwamura, M., Seirin-Lee, S., & Ei, S.-I. (2018). Dynamics of localized unimodal patterns in reaction-diffusion systems related to cell polarization by extracellular signaling. SIAM Journal on Applied Mathematics, 78(6), 3238–3257. https://doi.org/10.1137/18M1163749
Seirin-Lee, S., Tashiro, S., Awazu, A., & Kobayashi, R. (2017). A new application of the phase-field method for understanding the reorganization mechanisms of nuclear architecture. Journal of Mathematical Biology, 74, 333–354. https://doi.org/10.1007/s00285-016-1031-3
Seirin-Lee, S. (2016). Lateral inhibition-induced pattern formation controlled by the size and geometry of the cell. Journal of Theoretical Biology, 404, 51–65. https://doi.org/10.1016/j.jtbi.2016.05.025
^co-corresponding authors