RECODE
Resolution of the curse of dimensionality in single-cell RNA sequencing data analysis
Yusuke Imoto†, Tomonori Nakamura†, Emerson G. Escolar, Michio Yoshiwaki, Yoji Kojima, Yukihiro Yabuta, Yoshitaka Katou, Takuya Yamamoto, Yasuaki Hiraoka*, Mitinori Saitou*.
†equal contribution, *corresponding authors.
Life Science Alliance, August 9, 2022.
doi: 10.26508/lsa.202201591
Single-cell RNA sequencing (scRNA-seq) can determine gene expression in numerous individual cells simultaneously, promoting progress in the biomedical sciences. However, scRNA-seq data are high-dimensional with substantial technical noise, including dropouts. During analysis of scRNA-seq data, such noise engenders a statistical problem known as the curse of dimensionality (COD). Based on high-dimensional statistics, we herein formulate a noise reduction method, RECODE (resolution of the curse of dimensionality), for high-dimensional data with random sampling noise. We show that RECODE consistently eliminates COD in relevant scRNA-seq data with unique molecular identifiers. RECODE does not involve dimension reduction and recovers expression values for all genes, including lowly expressed genes, realizing precise delineation of cell-fate transitions and identification of rare cells with all gene information. Compared to other representative imputation methods, RECODE employs different principles and exhibits superior overall performance in cell-clustering and single-cell level analysis. The RECODE algorithm is parameter-free, data-driven, deterministic, and high-speed, and notably, its applicability can be predicted based on the variance normalization performance. We propose RECODE as a general strategy for preprocessing noisy high-dimensional data.
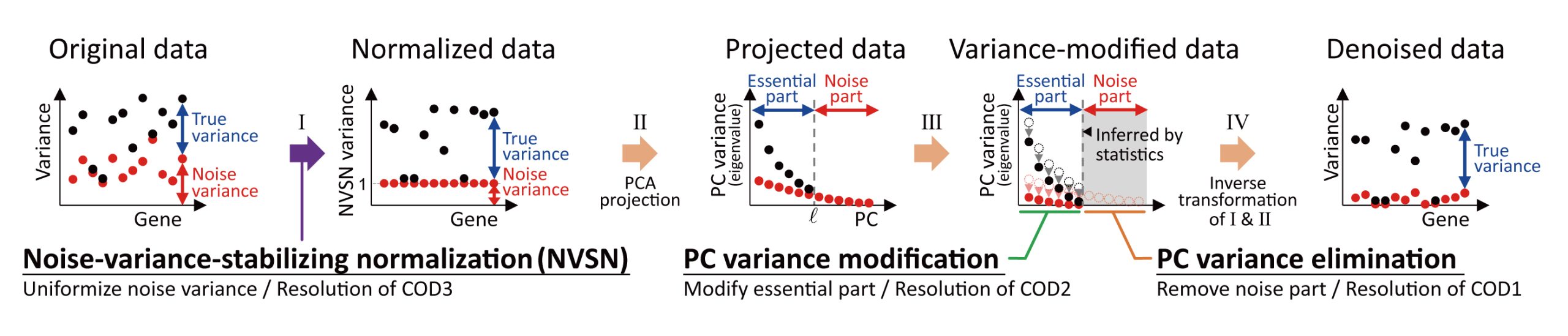
V-Mapper
Topological data analysis for high-dimensional data with velocity
Yusuke Imoto, Yasuaki Hiraoka.
Nonlinear Theory and Its Applications, IEICE, April 1, 2023.
doi: 10.1587/nolta.14.92
Mapper, a topological data analysis method for high-dimensional data, represents a topological structure as a simplicial complex or graph based on the nerve of clusters. We propose V-Mapper (velocity Mapper), an extension of Mapper, for high-dimensional data with velocity. V-Mapper simultaneously describes a topological structure and flow as a weighted directed graph (V-Mapper graph) by embedding velocity in the edges of the Mapper graph. We apply V-Mapper to single-cell gene expression data using a method for inferring the velocity of gene expression. Moreover, the application of the Hodge decomposition on graph enhances the interpretation of the flow within V-Mapper graph.
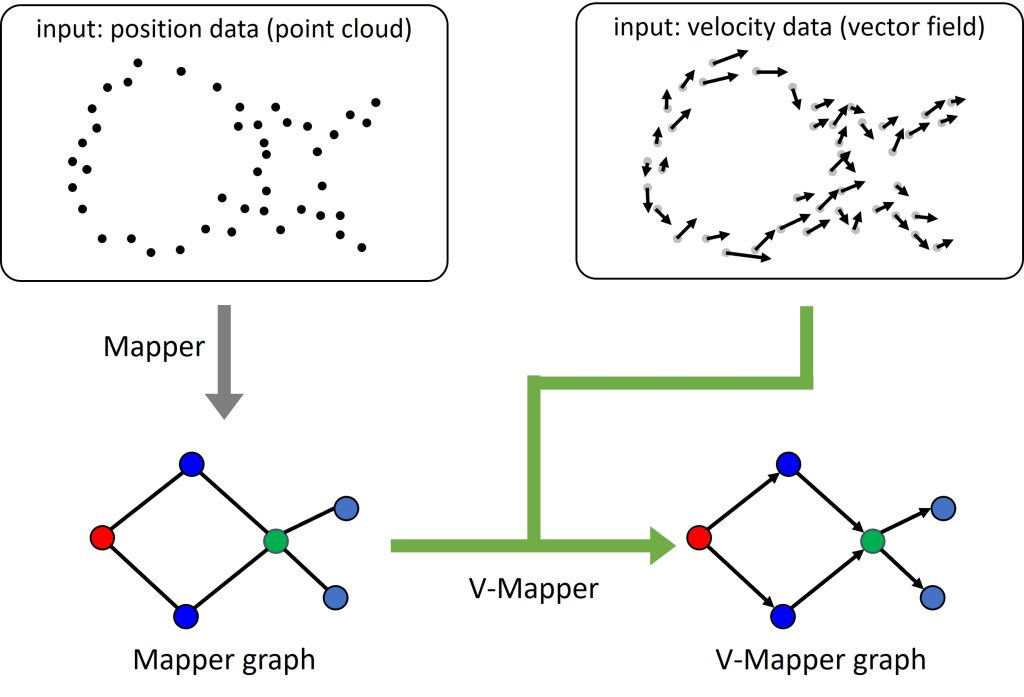
scEGOT
Single-cell trajectory inference framework based on entropic Gaussian mixture optimal transport
Toshiaki Yachimura, Hanbo Wang, Yusuke Imoto, Momoko Yoshida, Sohei Tasaki, Yoji Kojima, Yukihiro Yabuta, Mitinori Saitou, Yasuaki Hiraoka.
bioRxiv, September 14, 2023.
doi: 10.1101/2023.09.11.557102
Time-series single-cell RNA sequencing (scRNA-seq) data have opened a door to elucidate cell differentiation processes. In this context, the optimal transport (OT) theory has attracted attention to interpolate scRNA-seq data and infer the trajectories of cell differentiation. However, there remain critical issues in interpretability and computational cost. This paper presents scEGOT, a novel comprehensive trajectory inference framework for single-cell data based on entropic Gaussian mixture optimal transport (EGOT). By constructing a theory of EGOT via an explicit construction of the entropic transport plan and its connection to a continuous OT with its error estimates, EGOT is realized as a generative model with high interpretability and low computational cost, dramatically facilitating the inference of cell trajectories and dynamics from time-series data. The scEGOT framework provides comprehensive outputs from multiple perspectives, including cell state graphs, velocity fields of cell differentiation, time interpolations of single-cell data, space-time continuous videos of cell differentiation with gene expressions, gene regulatory networks, and reconstructions of Waddington’s epigenetic landscape. To demonstrate that scEGOT is a powerful and versatile tool for single-cell biology, we applied it to time-series scRNA-seq data of the human primordial germ cell-like cell (human PGCLC) induction system. Using scEGOT, we precisely identified the PGCLC progenitor population and the bifurcation time of the segregation. Our analysis suggests that a known marker gene TFAP2A alone is not sufficient to identify the PGCLC progenitor cell population, but that NKX1-2 is also required. In addition, we found that MESP1 and GATA6 may also be crucial for PGCLC/somatic cell segregation.
Topological Node2vec
Enhanced Graph Embedding via Persistent Homology
Yasuaki Hiraoka, Yusuke Imoto, Killian Meehan, Théo Lacombe, Toshiaki Yachimura.
arXiv, September 15, 2023.
doi: 10.48550/arXiv.2309.08241
Node2vec is a graph embedding method that learns a vector representation for each node of a weighted graph while seeking to preserve relative proximity and global structure. Numerical experiments suggest Node2vec struggles to recreate the topology of the input graph. To resolve this we introduce a topological loss term to be added to the training loss of Node2vec which tries to align the persistence diagram (PD) of the resulting embedding as closely as possible to that of the input graph. Following results in computational optimal transport, we carefully adapt entropic regularization to PD metrics, allowing us to measure the discrepancy between PDs in a differentiable way. Our modified loss function can then be minimized through gradient descent to reconstruct both the geometry and the topology of the input graph. We showcase the benefits of this approach using demonstrative synthetic examples.
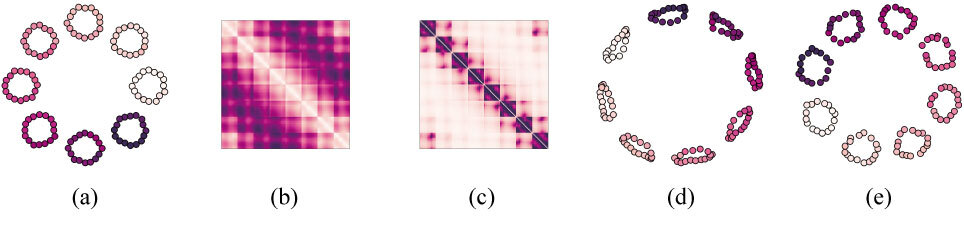
Figure 1. Illustration of Node2vec behavior with and without the incorporation of our topological loss during training. (a) An initial point cloud and (b) its corresponding pairwise distance matrix. (c) The weighted adjacency matrix obtained by inverting the pairwise distances. This is the graph used as input for Node2vec in this experiment. (d) The embedding proposed by Node2vec after training using only the standard reconstruction loss. It fails to properly retrieve the eight smaller cycles appearing in the input graph, and the emergent central cycle is far too large. (e) The embedding proposed by Node2vec after training while including our new topological loss term, in which the eight smaller cycles are recovered and the central cycle has been kept to a proper size.